ما هو أصغر حجم يمكن أن تدور فيه إبرة لتشير إلى الاتجاه المعاكس؟

في عالم الرياضيات الحديثة، قليلة هي المشكلات التي استحوذت على خيال المحللين والهندسيين مثل فرضية كاكييا. في جوهرها تكمن مسألة بسيطة: ما هو أصغر حجم يمكن فيه تدوير إبرة لتشير إلى كل الاتجاهات؟ هذا اللغز الهندسي أذهل الرياضيين لأكثر من قرن بسبب طبيعته البديهية الخادعة وآثاره العميقة في التحليل والهندسة وحتى علوم الحاسوب النظرية.

في أوائل عام 2025، تصدرت عناوين الأخبار الرياضياتية الصينية هونغ وانغ، إلى جانب زميلها المشارك جوشوا زال، بحل النسخة ثلاثية الأبعاد من فرضية كاكييا. يقدم عملهما، الذي يحمل عنوان ”تقديرات الحجم لاتحادات المجموعات المحدبة، وفرضية مجموعة كاكييا في ثلاثة أبعاد“، إجابة قاطعة لهذه المشكلة المستمرة ويلقي ضوءًا جديدًا على أحد الأسئلة الأساسية حول الفضاء والدوران والأبعاد. إلى جانب براعته النظرية، فإن النتيجة لها أيضًا صلة مباشرة بالحدس الفيزيائي: فهي تضفي الطابع الرسمي على فكرة أن تدوير إبرة بالكامل في الفضاء ثلاثي الأبعاد يتطلب مساحة ذات حجم كامل بالفعل — بدون حيل أو خدع.

فرضية كاكييا - لغز عمره قرن من الزمان:

طرح المشكلة لأول مرة في عام 1917 عالم الرياضيات الياباني سويشي كاكييا، الذي سأل: ما هي المساحة الدنيا في المستوى الذي يمكن فيها تدوير إبرة مقدار 360 درجة؟ كانت الإجابة صادمة. في عشرينيات القرن الماضي، أظهر عالم الرياضيات الروسي أبرام بيسكوفتش أنه من الممكن تدوير مثل هذه الإبرة في مجموعة من المساحات الاعتباطية الصغيرة، حتى تقترب من الصفر. بدت هذه المجموعات التي أطلق عليها اسم مجموعات بيسكوفتش متناقضة، فهي تسمح بالدوران الكامل في ”مساحة صفرية“، على الأقل من حيث المساحة.

أثارت هذه الحقيقة الغريبة أسئلة أعمق. بدأ علماء الرياضيات يتساءلون عن كيفية حدوث هذه الظاهرة في أبعاد أعلى. هل يمكن أن توجد مجموعات مماثلة في ثلاثة أبعاد؟ هل يمكن، من الناحية النظرية، تدوير عصا في كل اتجاه داخل منطقة ذات حجم صغير بشكل اعتباطي؟

أدى ذلك إلى ظهور فرضية كاكييا في n بُعد، والتي تنص على أن أي مجموعة جزئية من ℝⁿتحتوي على قطعة خطية وحدة في كل اتجاه يجب أن يكون لها بُعد هاوسدورف كامل n. بعبارة أخرى، لا يمكنك ”إخفاء“ كائن كامل الاتجاهات في فضاء لا يشغل أبعاده المحيطة بالكامل.

بينما تم إثبات الفرضية في بعدين، فإن الحالة ثلاثية الأبعاد - التي تبدو الأكثر بديهية - قاومت أفضل جهود الرياضيين لعقود. أي حتى عام 2025.

اختراق هونغ وانغ:

هونغ وانغ، أستاذة مشاركة في معهد كورانت بجامعة نيويورك (ومن المقرر أن تنضم إلى معهد الدراسات العليا العلمية في فرنسا)، كانت قد اكتسبت بالفعل سمعة طيبة في التحليل الهندسي. في شباط / فبراير 2025، أصدرت هي وزميلها المشارك جوشوا زال ورقة بحثية تقدم دليلاً كاملاً على فرضية كاكييا في ثلاثة أبعاد.

الرياضية هونغ وانغ في إحدى محاضراتها

جمعت منهجيتهما بين أدوات من الهندسة الجبرية وهندسة الوقوع والتحليل التوافقي، وهي مجالات تدرس كل منها الفضاء والبنية بطرق فريدة. كان أحد ابتكاراتهما الرئيسية هو تطوير تقديرات الحجم لمجموعات المجموعات المحدبة، ما وفر حدودًا دقيقة لمقدار المساحة التي تشغلها بالضرورة مجموعة من المقاطع الخطية التي تشير إلى كل اتجاه.

وقد سمح ذلك لوانغ وزال بإثبات قطعي أن أية مجموعة تحتوي على خط في كل اتجاه في الفضاء الثلاثي الأبعاد يجب أن يكون لها بُعد كامل. لا يمكن أن يكون هناك نظير ثلاثي الأبعاد لمجموعات بيسكوفتش الشبيهة بالفراكتلات في الفضاء الثنائي الأبعاد. باختصار: لا يمكنك تدوير إبرة في كل اتجاه في فضاء لا يشغل حجمًا كاملاً.

التطبيق - ماذا يعني ذلك بالنسبة لتدوير الإبرة:

نتائج وانغ لها تفسير فيزيائي قوي. عندما تسأل، ”ما هو أصغر حجم يمكن فيه تدوير الإبرة لتواجه الاتجاه المعاكس؟“ فإنك تسأل نسخة من سؤال كاكييا.

تؤكد أعمالها ذلك في الأبعاد الثلاثية:

• تحتاج إلى مساحة ذات حجم ثلاثي الأبعاد كامل.

• لا يوجد تكوين ذكي أو منطقة ”مسطحة“ تسمح لك بتدوير عصا في جميع الاتجاهات.

• أي نظام فيزيائي أو رياضي يسمح بحركة اتجاهية كاملة يجب أن يكون بطبيعته ثلاثي الأبعاد في هيكله.

تخيل ذراعًا آليًا في منطقة ضيقة، أو هوائيًا ساتليًا يحتاج إلى تغطية اتجاهية كاملة. يخبرنا عمل وانغ أن هناك حدًا أدنى هندسيًا صعبًا لمدى صغر المساحة اللازمة لهذا الدوران.

هذه ليست مجرد رؤية مجردة؛ بل لها صلة بالروبوتات والرسومات الحاسوبية والهندسة الميكانيكية وعلوم المواد، حيث غالبًا ما تكون الحركة الكاملة النطاق الموفرة للمساحة أمرًا بالغ الأهمية.

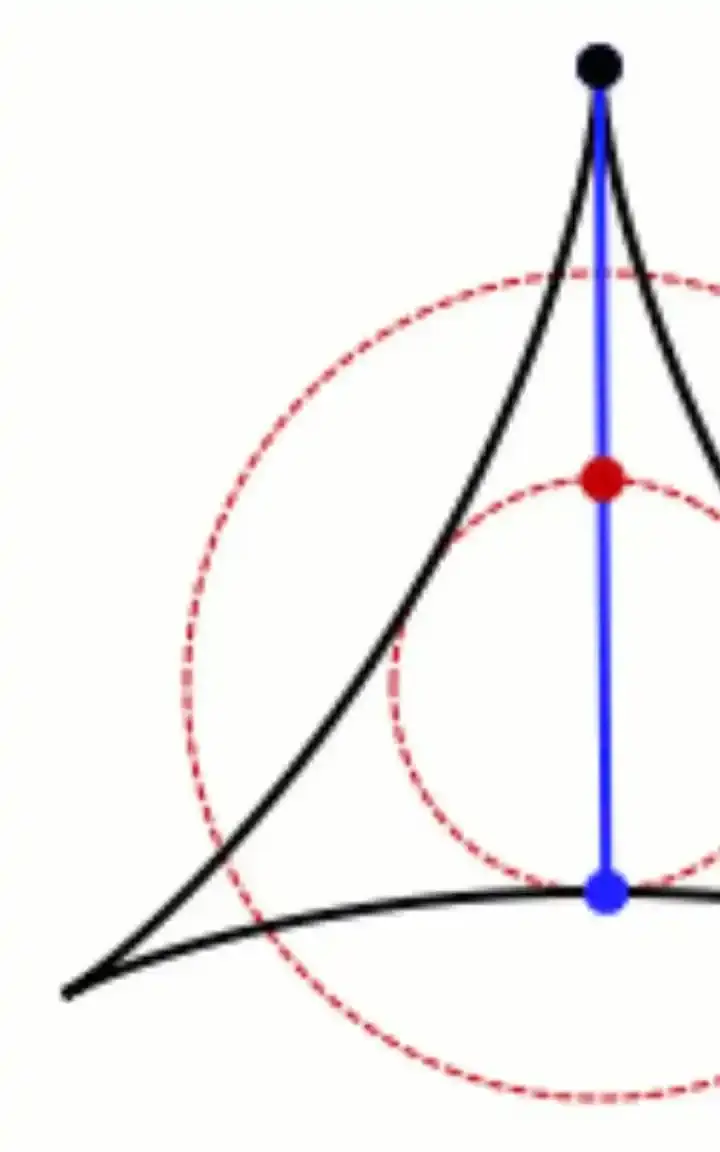
مسألة كاكييا – الإبرة باللون الأزرق ومسارها بالأسود

الأدوات الرياضية وراء الإثبات:

تكمن صعوبة مشكلة كاكييا في مزجها بين الهندسة والتحليل. استند اكتشاف وانغ وزال إلى عدة استراتيجيات رياضية رئيسية:

هندسة الوقوع:

دراسة كيفية تقاطع الأشكال الهندسية كالخطوط والمستويات والأنابيب. يساعد هذا في التحكم في عدد المرات التي يمكن أن تتداخل فيها خطوط اتجاهية مختلفة داخل مجموعة.

تقسيم كثيرات الحدود:

تقنية تستخدم لتقسيم المساحة إلى أجزاء يمكن التحكم فيها باستخدام أسطح كثيرات الحدود. وهي تساعد في تحليل كيفية انتشار المجموعات عبر المساحة.

تقديرات الحجم:

طورت وانغ وزال التقنيات السابقة من خلال الحصول على حدود أكثر دقة لمقدار الحجم الذي يجب أن تشغله اتحادات الأنابيب (الإبر المثالية). شكلت حدود الحجم هذه حجر الزاوية في حجتهم البعدية.

التحليل التوافقي وتحليل فورييه:

يستند العمل الجديد إلى أفكار من التحليل حول كيفية تصرف الدوال والإشارات في الفضاء والتردد، وهي مرتبطة ارتباطًا وثيقًا ببنية مجموعات كاكييا.

نجمة رياضيات صاعدة:

حل هونغ وانغ لفرضية كاكييا ثلاثية الأبعاد قد قفز بها إلى صدارة عالم الرياضيات العالمي، وتعتبر على نطاق واسع منافسة محتملة على ميدالية فيلدز. لا تمثل مساهماتها انتصارات تقنية فحسب، بل تذكرنا أيضًا بكيفية استمرار الرياضيين الشباب في إعادة صياغة الأسئلة القديمة.

إلى جانب المعادلات والنظريات، تتناول أعمال وانغ هندسة الاحتمالات: كيف تتحرك الأشياء، وكم تحتاج الحركة من مساحة، وأين تقع حدود الحصر.

من خلال حل فرضية كاكييا ثلاثية الأبعاد، أظهرت أن حتى أصغر الحركات — مثل دوران إبرة — تخضع للبنية العميقة للفضاء نفسه.